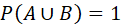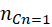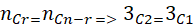Quantitative Aptitude - Permutation & Combination - Formula & Concept Tutorial
- Factorial Notation:
Let n be a positive integer. Then, factorial n, denoted n! is defined as:
n! = n(n - 1)(n - 2) ... 3.2.1.
For example
- 5! = ( 5 * 4 * 3 * 2 * 1 ) = 120
- 1! = (1) = 1
- 0! = 1
- Permutations:
The different arrangements of a given number of things by taking some or all at a time, are called permutations.
Examples:
- All permutations made with the letters a, b, c by taking two at a time are (ab, ba, ac, ca, bc, cb)
Here n ( total no. of letter ) = 3 , r ( taking two at a time ) = 2
This can be calculated using formula
No. of permutation of n things taken at a time.
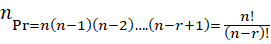
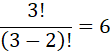
This 6 arrangement are (ab, ba, ac, ca, bc, cb)
- All permutations made with the letters a, b, c taking all at a time are n!:
( abc, acb, bac, bca, cab, cba)
Here n and r both are same i.e 3
So by using formula
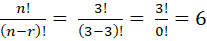
- Combinations:
Each of the different groups or selections which can be formed by taking some or all of a number of objects is called a combination.
Examples:
Suppose we want to select two out of three boys A, B, C. Then, possible selections are AB, BC and CA.
Note: AB and BA represent the same selection (combination) but different permutation.
No. Of Combination - 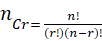
- Number of permutation of n object =>

- If A and B are exhaustive event then